椭圆函数
$\quad\\$
椭圆函数的概念
$\quad\\$
定义1$\quad$椭圆函数是指在$\mathbb{C}$上具有双周期$\omega_1,\omega_2$且满足$\displaystyle\text{Im}\frac{\omega_1}{\omega_2}>0$的亚纯函数
对于具有双周期$\omega_1,\omega_2$的椭圆函数$f(z)$,易知其任意一个周期$\omega$都可以表示为$\omega=n_1\omega_1+n_2\omega_2\quad n_1,n_2\in \mathbb{Z}$的形式,将$f(z)$所有的周期归入一个集合$M=\{n_1\omega_1+n_2\omega_2|n_1,n_2\in \mathbb{Z}\}$中,称此集合为以$(\omega_1,\omega_2)$为基的函数$f(z)$的周期模
对于$\mathbb{C}$上任意一点$a$,称集合$P=\{a+t_1\omega_1+t_2\omega_2|t_1,t_2\in [0,1)\}$为$f(z)$的一个基本平行四边形,由于$f(z)$为$\mathbb{C}$上双周期函数,故通过$f(z)$在$P$上的性质就能了解其在$\mathbb{C}$上的性质
$$\quad\\$$
若$f(z)$在$\mathbb{C}$上解析,取$f(z)$的任意一个基本平行四边形$P$,由于$\overline{P}$为紧集,$f(z)$在$\overline{P}$上连续,故$f(z)$在$\overline{P}$上有界,即在$\mathbb{C}$上有界,由刘维尔定理有
定理1$\quad$无极点的椭圆函数必为常数
$$\quad\\$$
虽然非常数的椭圆函数必有极点,但易知其极点有限,取$f(z)$的任意一个基本平行四边形$P$,假设$f(z)$在$\overline{P}$上有无穷多个极点,由Bolzano-Weierstrass定理,在$\overline{P}$中至少存在一个极点集的聚点,与极点的孤立性矛盾,故$f(z)$在$\overline{P}$上只有有限个极点;同样,取函数$g(z)=1/f(z)$,并在$f(z)$的极点处补充定义$g(z)=0$,易知$g(z)$在$\mathbb{C}$上亚纯,且其只有孤立极点,故$f(z)$在$\overline{P}$上只有有限个零点,总结如下
定理2$\quad$椭圆函数在其任一基本平行四边形上只有有限个极点和零点
$$\quad\\$$
既然极点数目有限,则可以选取基本平行四边形$P$,使得$f(z)$在$\partial P$上没有极点,此时$f(z)$在$P$内极点上的留数之和为$\displaystyle\frac{1}{2\pi i}\int_{\partial P}f(z)\text{d}z$,此积分沿平行四边形对边的分段积分互相抵消,因此结果为零,故有
定理3$\quad$椭圆函数的留数之和为零
$$\quad\\$$
考虑函数$g(z)=f’(z)/f(z)$,由留数部分内容知$f(z)$的零点与极点均为$g(z)$的单极点,且$g(z)$在$f(z)$零点的留数为其级,在$f(z)$极点的留数为其级的相反数,又$g(z)$为椭圆函数,其极点留数之和为零,故有
定理4$\quad$椭圆函数的零点数与极点数相等(几级算几个)
$$\quad\\$$
由于函数$f(z)-C(C$为任意常数$)$与$f(z)$具有相同极点数,故二者也具有相同零点数,即
定理5$\quad$椭圆函数取到$\overline{\mathbb{C}}$所有值的次数相同(几级算几个)
$$\quad\\$$
定义2$\quad$称椭圆函数在基本平行四边形上取到任意常数$C$的次数为其阶数(计重数),由定理3可知,任一椭圆函数的阶数至少为二
$$\quad\\$$
选取基本平行四边形$P$,使得$f(z)$在$\partial P$上没有极点,由留数部分内容,
$\displaystyle \frac{1}{2\pi i}\int_{\partial P}\frac{zf’(z)}{f(z)}\text{d}z=\sum_{k=1}^{n}\alpha_ka_k-\sum_{j=1}^{m}\beta_jb_j$,其中$a_k$为$f(z)$零点,$b_j$为$f(z)$极点,$\alpha_k,\beta_j$分别为其级,根据$f(z)$的周期性,左边积分为
$\displaystyle \frac{1}{2\pi i}\left[\left(\int_{a}^{a+\omega_1}-\int_{a+\omega_2}^{a+\omega_1+\omega_2}\right)+\left(\int_{a+\omega_1}^{a+\omega_1+\omega_2}-\int_{a}^{a+\omega_2}\right)\right]\frac{zf’(z)}{f(z)}\text{d}z$
$=\omega_1$$\displaystyle\frac{1}{2\pi i}\int_{a}^{a+\omega_2}\frac{f’(z)}{f(z)}\text{d}z$$-\omega_2$$\displaystyle\frac{1}{2\pi i}\int_{a}^{a+\omega_1}\frac{f’(z)}{f(z)}\text{d}z$
两个紫色的积分表示$f(z)$描出的闭曲线环绕原点的卷绕数,因此为整数,整个积分结果即为函数$f(z)$的一个周期,故有
定理6$\quad$椭圆函数$f(z)$在基本平行四边形上的零点之和与极点之和的差(几级算几次)为$f(z)$的一个周期
$\quad\\$
Weierstrass椭圆函数
$\quad\\$
由以上讨论可知,最简单的椭圆函数是二阶的,这样的函数在基本平行四边形中具有一个二级极点或者两个单极点,维尔斯特拉斯从构造具有二级极点的函数出发发展出一套理论,而雅可比则研究两个单极点的情况,我们先沿维尔斯特拉斯的道路出发,以后将会看到雅可比的理论更多地用于解决实际问题,而维尔斯特拉斯的理论在理论发展中应用更为方便
$$\quad\\$$
引理1$\quad$设$\omega=n_1\omega_1+n_2\omega_2$为椭圆函数$f(z)$的周期,则级数$\displaystyle\sum_{\omega\neq 0}\frac{1}{|\omega|^{\alpha}}$在$\alpha>2$时收敛
$\nabla$证
$$
记P_n为中心在原点,有两个顶点为n(\omega_1+\omega_2),n(\omega_1-\omega_2)的平行四边形\\
\quad\\
易知在f(z)在\partial P_n上有8n个周期\\
\quad\\
令原点到\partial P_1的距离为\delta,则其到\partial P_n的距离为n\delta\\
\quad\\
故\sum_{\omega\neq 0}\frac{1}{|\omega|^{\alpha}}\le \sum_{\omega\in \partial P_n}\frac{8n}{(n\delta)^{\alpha}}=\sum_{\omega\in \partial P_n}\frac{8}{\delta^{\alpha}}\frac{1}{n^{\alpha-1}}\\
\quad\\
易知此级数在\alpha>2时收敛\qquad\square
$$
$$\quad\\$$
由引理1可知级数$\displaystyle\sum_{\omega\neq 0}\left[\frac{1}{(z-\omega)^{2}}-\frac{1}{\omega^{2}}\right]$在与$f(z)$周期模$M$不交的紧集上一致收敛。事实上,由于级数的收敛性不受其初始有限项的影响,对任意$R>0$,不妨设$|\omega|>2R$,在$|z|\le R$中有$\displaystyle\left|\frac{1}{(z-\omega)^{2}}-\frac{1}{\omega^{2}}\right|=\left|\frac{z(2\omega-z)}{\omega^2(z-\omega)^{2}}\right|\le\left|\frac{10R}{\omega^3}\right|$,易知结论成立。由此我们可以引入如下函数
$$\quad\\$$
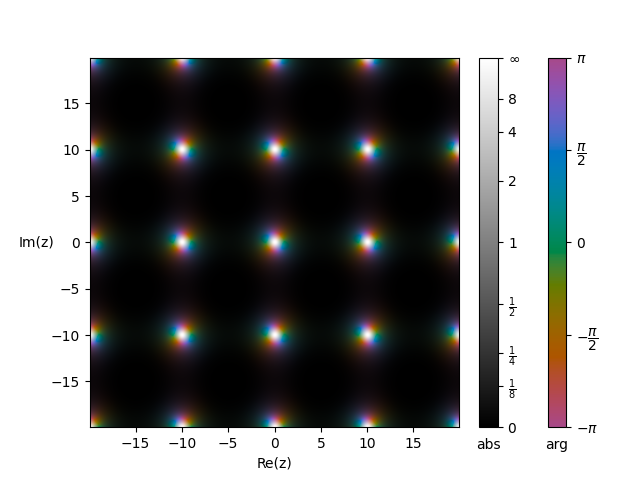
定义3$\quad$称如下函数为维尔斯特拉斯$\wp$函数
$$\wp(z)=\frac{1}{z^2}+\sum_{\omega\neq 0}\left[\frac{1}{(z-\omega)^{2}}-\frac{1}{\omega^{2}}\right]$$
由上文可知$\wp(z)$为$\mathbb{C}$上亚纯函数,其导数为
$$\wp’(z)=-2\sum_{\omega}\frac{1}{(z-\omega)^{3}}$$
$\wp’(z)$在$z\notin M$时绝对收敛,因此也为$\mathbb{C}$上亚纯函数,又$\wp’(z+\omega_1)$和$\wp’(z+\omega_2)$只是$\wp’(z)$级数的重排,故$\wp’(z+\omega_1)=\wp’(z+\omega_2)=\wp’(z)$,可知$\wp’(z)$为椭圆函数
对等式积分有$\wp(z+\omega_1)=\wp(z)+C$,令$z=-\omega_1/2$可得
$\wp(\omega_1/2)=\wp(-\omega_1/2)+C$,因为$\wp(z)$为偶函数,故$C=0$,同理对$\omega_2$有$\wp(z+\omega_2)=\wp(z)$,因此$\wp(z)$为具有周期$\omega_1,\omega_2$的二阶椭圆函数,其极点
$z=\omega=n_1\omega_1+n_2\omega_2\quad n_1,n_2\in\mathbb{Z}$均为二级极点,且互相等价
当$\omega_1=10,\omega_2=10i$时其图像如下
作出$\wp(z)$在$z=0$处的洛朗展式
$$\begin{aligned}\wp(z)&=\frac{1}{z^2}+\sum_{\omega\neq 0}\left[\frac{1}{\omega^2}\left(1+\frac{z}{\omega}+\left(\frac{z}{\omega}\right)^2+\cdots\right)^2-\frac{1}{\omega^{2}}\right]\\
\quad\\
&=\frac{1}{z^2}+\sum_{\omega\neq 0}\left[\frac{1}{\omega^2}\left(1+2\frac{z}{\omega}+3\left(\frac{z}{\omega}\right)^2+\cdots\right)-\frac{1}{\omega^{2}}\right]\\
\quad\\
&=\frac{1}{z^2}+\sum_{k=1}^{\infty}c_kz^k\qquad c_k=(k+1)\sum_{\omega\neq 0}\frac{1}{\omega^{k+2}}\end{aligned}$$
由$\omega$的对称性易知当$k$为奇数时,$c_k=0$,故$\wp(z)$在$z=0$处的洛朗展式可简化为
$$\wp(z)=\frac{1}{z^2}+\sum_{m=1}^{\infty}c_mz^{2m}\qquad c_m=(2m+1)\sum_{\omega\neq 0}\frac{1}{\omega^{2m+2}}$$
引入记号$b_m=\displaystyle\sum_{\omega\neq 0}\frac{1}{\omega^{m}}$,则有$\wp(z)=\displaystyle\frac{1}{z^2}+3b_4z^2+5b_6z^4+\cdots$
$\wp’(z)=\displaystyle-\frac{2}{z^3}+6b_4z+20b_6z^3+\cdots$,构造$\wp(z)$与$\wp’(z)$的多项式$P(z)$,使其不含极点,可取$P(z)=\wp’^2(z)-4\wp^3(z)+60b_4\wp(z)$,由于$P(z)$为椭圆函数且不含极点,故其为常数,取出表达式中常数项相加得到$P(z)=-140b_6$,令$g_2=60b_4,g_3=140b_6$,可得如下微分方程
$$\wp’^2(z)=4\wp(z)^3-g_2\wp(z)-g_3$$
令$u=\wp(z)$,解如上微分方程可得
$$z=\int_{\infty}^{u}\frac{\text{d}u}{\sqrt{u^3-g_2u-g_3}}$$
这表明$\wp(z)$是椭圆积分的逆,很明显,积分中根号下的多项式不能有重根,否则此积分将有初等表达式,事实上,设此多项式的三个根分别为$e_1,e_2,e_3$,则有
$$\wp’^2(z)=4(\wp(z)-e_1)(\wp(z)-e_2)(\wp(z)-e_3)$$
因为$\wp(\omega_1-z)=\wp(-z)=\wp(z)$,故$-\wp’(\omega_1-z)=\wp’(z)$,令$z=\omega_1/2$,则有$\wp’(\omega_1/2)=0$,同样,$\wp’(\omega_2/2)=0$,$\wp’((\omega_1+\omega_2)/2)=0$,故有
$$\displaystyle e_1=\wp(\frac{\omega_1}{2})\quad e_2=\wp(\frac{\omega_2}{2})\quad e_3=\wp(\frac{\omega_1+\omega_2}{2})$$
由于$\wp’(z)$为三阶椭圆函数,故$\omega_1/2,\omega_2/2,(\omega_1+\omega_2)/2$是$\wp’(z)$的一级零点,即$\wp(z)$在基本平行四边形上以重数二取这三个值,若其中有两个值相同,则$\wp(z)$取同一个值四次,这与$\wp(z)$为二阶椭圆函数矛盾,故这三个根互异,且由微分方程有
$$e_1+e_2+e_3=0\quad
e_1e_2+e_2e_3+e_3e_1=-\frac{g_2}{4}\quad
e_1e_2e_3=\frac{g_3}{4}$$
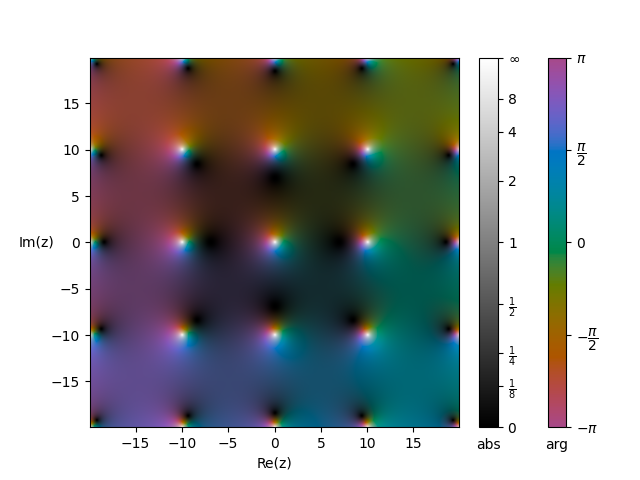
由于$\wp(z)$仅有零留数,故其为某一单值函数的导数,习惯上记此函数为$-\zeta(z)$,直接对$\wp(z)$的表达式积分并加以规格化使其成为奇函数可得
$$\zeta(z)=\frac{1}{z}+\sum_{\omega\neq 0}\left(\frac{1}{z-\omega}+\frac{1}{\omega}+\frac{z}{\omega^2}\right)$$
由证明$\wp(z)$收敛的方法,设$|\omega|>2R>0$,在$|z|\le R$中有
$\displaystyle\left|\frac{1}{z-\omega}+\frac{1}{\omega}+\frac{z}{\omega^2}\right|=\left|\frac{z^2}{\omega^2(z-\omega)}\right|\le \left|\frac{2R^2}{\omega^3}\right|$,易知$\zeta(z)$中级数在$\mathbb{C}$上任意不包含极点(即$\wp(z)$极点)的紧集上一致收敛,故$\zeta(z)$也为$\mathbb{C}$上亚纯函数
因为$\zeta’(z)=-\wp(z)$,故有$\zeta’(z+\omega_1)=\zeta’(z)$,积分得
$\zeta(z+\omega_1)=\zeta(z)+\eta_1$,令$z=-\displaystyle\frac{\omega_1}{2}$有$\eta_1=2\zeta(\displaystyle\frac{\omega_1}{2})$,同样,$\eta_2=2\zeta(\displaystyle\frac{\omega_2}{2})$,对$\zeta(z)$在边界不含极点的基本平行四边形$P$的边界$\partial P$上进行环路积分,由级数表达式有$\displaystyle\int_{\partial P}\zeta(z)\text{d}z=2\pi i$,又
$\displaystyle\int_{\partial P}\zeta(z)\text{d}z=\left[\left(\int_{a}^{a+\omega_1}-\int_{a+\omega_2}^{a+\omega_1+\omega_2}\right)+\left(\int_{a+\omega_1}^{a+\omega_1+\omega_2}-\int_{a}^{a+\omega_2}\right)\right]\zeta(z)\text{d}z$
$=\eta_1\omega_2-\eta_2\omega_1$,我们得到如下Legendre关系
$$\eta_1\omega_2-\eta_2\omega_1=2\pi i$$
其中$\eta_1,\eta_2$称为$\zeta(z)$的基本准周期
当$\omega_1=10,\omega_2=10i$时其图像如下
继续对$\zeta(z)$进行积分,由于积分结果为多值对数函数,故用指数函数来消除多值性,且将积分后级数每项减去常数$\ln(-\omega)$以保证其收敛性,记
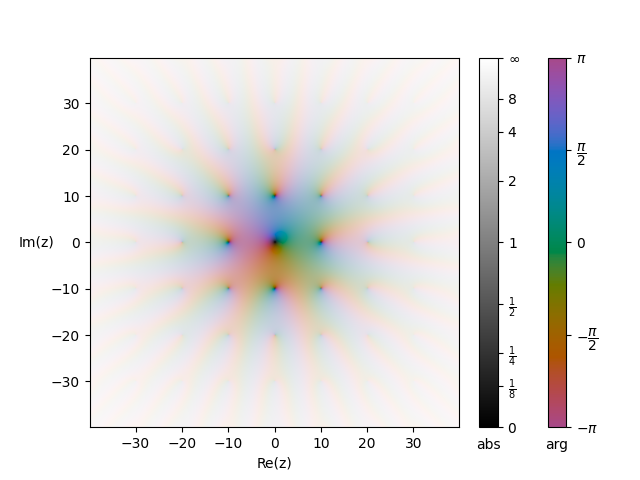
$\sigma(z)=\exp\left[{\displaystyle\int\zeta(z)}-\displaystyle\sum_{\omega\neq 0}\ln(-\omega)\right]$,即$\displaystyle\frac{\sigma’(z)}{\sigma(z)}=\zeta(z)$,可得其典范乘积表达式如下
$$\sigma(z)=z\prod_{\omega\neq 0}\left(1-\frac{z}{\omega}\right)e^{\frac{z}{\omega}+\frac{1}{2}\left(\frac{z}{\omega}\right)^2}$$
$$\quad\\$$
引理2$\quad$令$E(z)=(1-z)e^{z+z^2/2}$,则$\forall |z|\le \displaystyle\frac{1}{2},|E(z)-1|\le 2|z|^3$
$\nabla$证
$$
易知当|z|<\frac{1}{2}时,E(z)=e^{g(z)}\quad g(z)=-\sum_{k=3}^{\infty}\frac{z^k}{k}\\
\quad\\
|g(z)|\le \sum_{k=3}^{\infty}\frac{|z|^k}{3}=\frac{|z|^3}{3}\frac{1}{1-|z|}\le \frac{2|z|^3}{3}\\
\quad\\
由以下两个不等式\\
\quad\\
|e^z-1|\le e^{|z|}-1\qquad e^x-1\le xe^x \quad \text{for}\; x\ge 0\\
\quad\\
有|E(z)-1|\le E^{|g(z)|}-1\le |g(z)|e^{|g(z)|}\le 2|z^3|
$$
$$\quad\\$$
同样设$|\omega|>2R>0$,$|z|\le R$,由引理2,$\sigma(z)$中无穷乘积在任意紧集上绝对收敛且一致收敛,故$\sigma(z)$为$\mathbb{C}$上整函数
当$\omega_1=10,\omega_2=10i$时其图像如下,其中模作了对数$|w|=\ln (1+|w|)$处理
由$\zeta(z)$的准周期性,$\displaystyle\frac{\sigma’(z+\omega_1)}{\sigma(z+\omega_1)}=\frac{\sigma’(z)}{\sigma(z)}+\eta_1$,积分有
$\ln \sigma(z+\omega_1)=\ln \sigma(z)+\eta_1 z+C$,令$\displaystyle z=-\frac{\omega_1}{2}$,因为$\sigma(z)$为奇函数,可得$\displaystyle C=\frac{1}{2}\eta_1\omega_1+\pi i$,即$\displaystyle\sigma(z+\omega_1)=-\sigma(z)e^{\eta_1(z+\frac{\omega_1}{2})}$,同理
$\displaystyle\sigma(z+\omega_2)=-\sigma(z)e^{\eta_2(z+\frac{\omega_2}{2})}$
$$\quad\\$$
定理7$\quad$设$f(z)$为任一$n$阶椭圆函数,其在一基本平行四边形上的所有零点为$a_k,1\le k\le n$,极点为$b_k,1\le k\le n$,则存在常数$c$,使得$f(z)$可表示为如下形式
$$f(z)=c\prod_{k=1}^{n}\frac{\sigma(z-a_k)}{\sigma(z-b_k)}$$
$\nabla$证
$$
令\Omega=\sum_{k=1}^{n} a_k-\sum_{k=1}^{n} b_k\\
\quad\\
再令F(z)=\left[\prod_{k=1}^{n-1}\frac{\sigma(z-a_k)}{\sigma(z-b_k)}\right]\frac{\sigma(z-a_n)}{\sigma(z-b_n-\Omega)}\\
\quad\\
易知F(z)以a_k为零点,以b_k为极点\\
\quad\\
又\sigma(z+\omega_1)=-\sigma(z)e^{\displaystyle\eta_1(z+\frac{\omega_1}{2})},\sigma(z+\omega_2)=-\sigma(z)e^{\displaystyle\eta_2(z+\frac{\omega_2}{2})}\\
\quad\\
有F(z+\omega_1)=F(z)\frac{e^{\displaystyle-\eta_1\sum_{k=1}^{n} a_k}}{e^{\displaystyle-\eta_1\sum_{k=1}^{n} b_k-\eta_1\Omega}}=F(z)\\
\quad\\
同理,F(z+\omega_2)=F(z)\frac{e^{\displaystyle-\eta_2\sum_{k=1}^{n} a_k}}{e^{\displaystyle-\eta_2\sum_{k=1}^{n} b_k-\eta_2\Omega}}=F(z)\\
\quad\\
易知f(z)与F(z)有相同的周期\\
\quad\\
故f(z)/F(z)为无极点的椭圆函数,因此为常数,即f(z)=cF(z)\\
\quad\\
由于\Omega=\omega\\
\quad\\
总可以选取恰当的基本平行四边形使\Omega=0\\
\quad\\
此时f(z)=cF(z)=c\prod_{k=1}^{n}\frac{\sigma(z-a_k)}{\sigma(z-b_k)}\qquad\square
$$
$$\quad\\$$
取$u\in\mathbb{C} \& u\notin M$,则$\wp(z)-\wp(u)$零点为$\pm u$,二级极点为$0$,由定理7,
$\displaystyle\wp(z)-\wp(u)=c\frac{\sigma(z-u)\sigma(z+u)}{\sigma^{2}(z)\sigma^{2}(u)}$,除以$\sigma^{2}(u)$是以防$\pm u$不在基本平行四边形中,令$z=0$即可得$c=-1$,即
$$\wp(z)-\wp(u)=-\frac{\sigma(z-u)\sigma(z+u)}{\sigma^{2}(z)\sigma^{2}(u)}$$
$\quad\\$
Jacobi椭圆函数
$\quad\\$
记$\omega_3=\omega_1+\omega_2$,$\eta_3=\eta_1+\eta_2$,由上节内容,
$\displaystyle\wp(z)-e_k=\wp(z)-\wp(\frac{\omega_k}{2})=\frac{\sigma^2(\displaystyle z-\frac{\omega_k}{2})e^{\eta_kz}}{\sigma^2(z)\sigma^2(\displaystyle\frac{\omega_k}{2})}=\frac{\sigma^2(\displaystyle z+\frac{\omega_k}{2})e^{-\eta_kz}}{\sigma^2(z)\sigma^2(\displaystyle\frac{\omega_k}{2})}$
令$\displaystyle\sigma_k(z)=-\frac{\sigma(\displaystyle z-\frac{\omega_k}{2})e^{\eta_kz/2}}{\sigma(\displaystyle\frac{\omega_k}{2})}=\frac{\sigma(\displaystyle z+\frac{\omega_k}{2})e^{-\eta_kz/2}}{\sigma(\displaystyle\frac{\omega_k}{2})}$,则有
$\displaystyle\wp(z)-e_k=\left(\frac{\sigma_k(z)}{\sigma(z)}\right)^2$,易知$\sigma_k(z)$为偶函数,且有
$$\displaystyle\sigma_k(z+\omega_k)=-\sigma_k(z)e^{\eta_k(z+\omega_k/2)}\\
\quad\\
\displaystyle\sigma_k(z+\omega_h)=\sigma_k(z)e^{\eta_h(z+\omega_h/2)} \qquad\text{for} \quad h\neq k$$
由微分方程$\wp’^2(z)=4(\wp(z)-e_1)(\wp(z)-e_2)(\wp(z)-e_3)$有
$\displaystyle\wp’^2(z)=4\left(\frac{\sigma_1(z)\sigma_2(z)\sigma_3(z)}{\sigma^3(z)}\right)^2$,比较原点处奇异部分可得
$\displaystyle\wp’(z)=-2\frac{\sigma_1(z)\sigma_2(z)\sigma_3(z)}{\sigma^3(z)}$
$$\quad\\$$
定义4$\quad$记$\displaystyle\lambda=\sqrt{e_1-e_2},t=\frac{z}{\lambda}$,称下列函数为雅可比椭圆函数
$$\text{sn}\,z=\lambda\frac{\sigma(t)}{\sigma_2(t)}\qquad\text{cn}\,z=\frac{\sigma_1(t)}{\sigma_2(t)}\qquad\text{dn}\,z=\frac{\sigma_3(t)}{\sigma_2(t)}$$
容易验证,$\text{sn}(z+\lambda\omega_1)=-\text{sn}\,z\qquad\text{sn}(z+\lambda\omega_2)=\text{sn}\,z$,故$\text{sn}\,z$的周期为$2\lambda\omega_1$和$\lambda\omega_2$,同理,$\text{cn}\,z$的周期为$2\lambda\omega_1$和$\lambda\omega_3$,$\text{dn}\,z$的周期为$\lambda\omega_1$和$2\lambda\omega_2$,易知其周期只与$\displaystyle\tau=\frac{\omega_2}{\omega_1}$有关,而与$\omega_1,\omega_2$绝对大小无关,事实上这三个雅可比椭圆函数也仅由$\tau$决定
令$\displaystyle K_1=\frac{\lambda\omega_1}{2},iK_2=\frac{\lambda\omega_2}{2}$,易知
| $\qquad\qquad$ | 极点 | 零点 | 周期 | |
|---|---|---|---|---|
| $\text{sn}\,z$ | $\qquad$ | $iK_2$,$2K_1+iK_2$ | $0$,$2K_1$ | $4K_1$,$2iK_2$ |
| $\text{cn}\,z$ | $\qquad$ | $iK_2$,$2K_1+iK_2$ | $K_1$,$3K_1$ | $4K_1$,$2K_1+2iK_2$ |
| $\text{dn}\,z$ | $\qquad$ | $iK_2$,$3iK_2$ | $K_1+iK_2$,$K_1+3iK_2$ | $2K_1$,$4iK_2$ |
| $\qquad\qquad$ | $\qquad\qquad$ | 图像($\tau=i$) |
|---|---|---|
| $\text{sn}\,z$ | $\qquad$ | 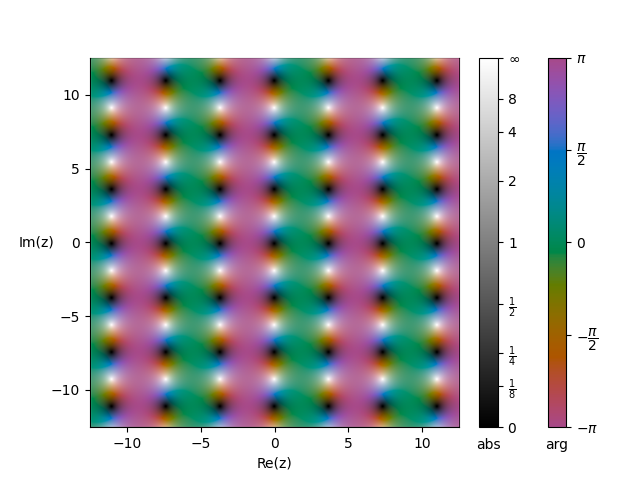 |
| $\text{cn}\,z$ | $\qquad$ | 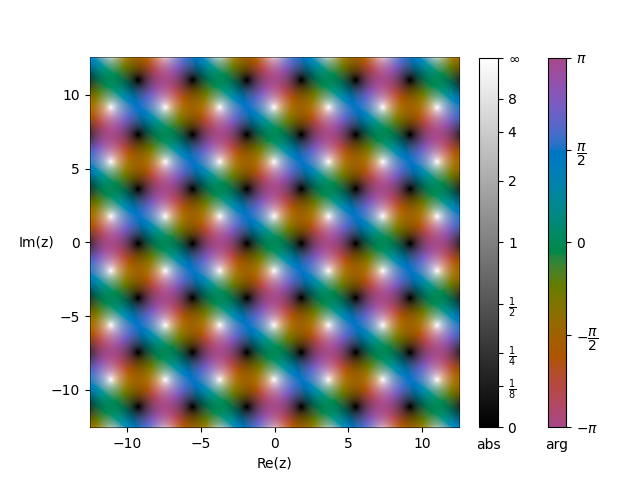 |
| $\text{dn}\,z$ | $\qquad$ | 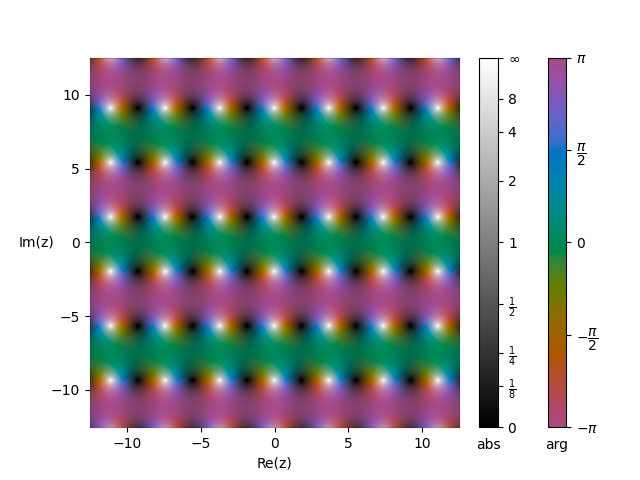 |
$\quad$
这三个函数均为二阶椭圆函数,且极点与零点均为一级,
由$\displaystyle\wp(z)-e_k=\frac{\sigma_k^2(z)}{\sigma^2(z)}$,
$\displaystyle e_1-e_2=\frac{\sigma_2^2(z)}{\sigma^2(z)}-\frac{\sigma_1^2(z)}{\sigma^2(z)}$,$\displaystyle e_3-e_2=\frac{\sigma_2^2(z)}{\sigma^2(z)}-\frac{\sigma_3^2(z)}{\sigma^2(z)}$,即
$$\text{sn}^2\,z+\text{cn}^2\,z=1\qquad k^2\text{sn}^2\,z+\text{dn}^2\,z=1$$
其中$\displaystyle k=\sqrt{\frac{e_3-e_2}{e_1-e_2}}$称为模常数,仅由周期比$\displaystyle\tau=\frac{\omega_2}{\omega_1}$决定
再对$\displaystyle\wp(z)-e_2=\frac{\sigma_2^2(z)}{\sigma^2(z)}$微分可得,$\displaystyle-2\frac{\sigma_1(z)\sigma_2(z)\sigma_3(z)}{\sigma^3(z)}=-2\frac{1}{\text{sn}^3\,z}\cdot\text{sn}’\,z$
即$\text{sn}’\,z=\text{cn}\, z\cdot\text{dn}\,z$,与上面的等式联立有
$\text{cn}’\,z=-\text{sn}\, z\cdot\text{dn}\,z$,$\text{dn}’\,z=-k^2\text{sn}\, z\cdot\text{cn}\,z$
将$\text{sn}’\,z=\text{cn}\, z\cdot\text{dn}\,z$平方消去$\text{cn}\, z,\text{dn}\,z$,令$\text{sn}\,z=w$有
$\displaystyle\frac{\text{d}w}{\text{d}z}=\sqrt{(1-w^2)(1-k^2w^2)}$,即
$$z=\int_{0}^{w}\frac{\text{d}u}{\sqrt{(1-u^2)(1-k^2u^2)}}$$
这说明$\text{sn}\,z$是椭圆积分的逆,由Schwarz-Christoff公式,当$0< k<1$时,此积分将$w$平面的上半平面共形映为$z$平面的一个长方形
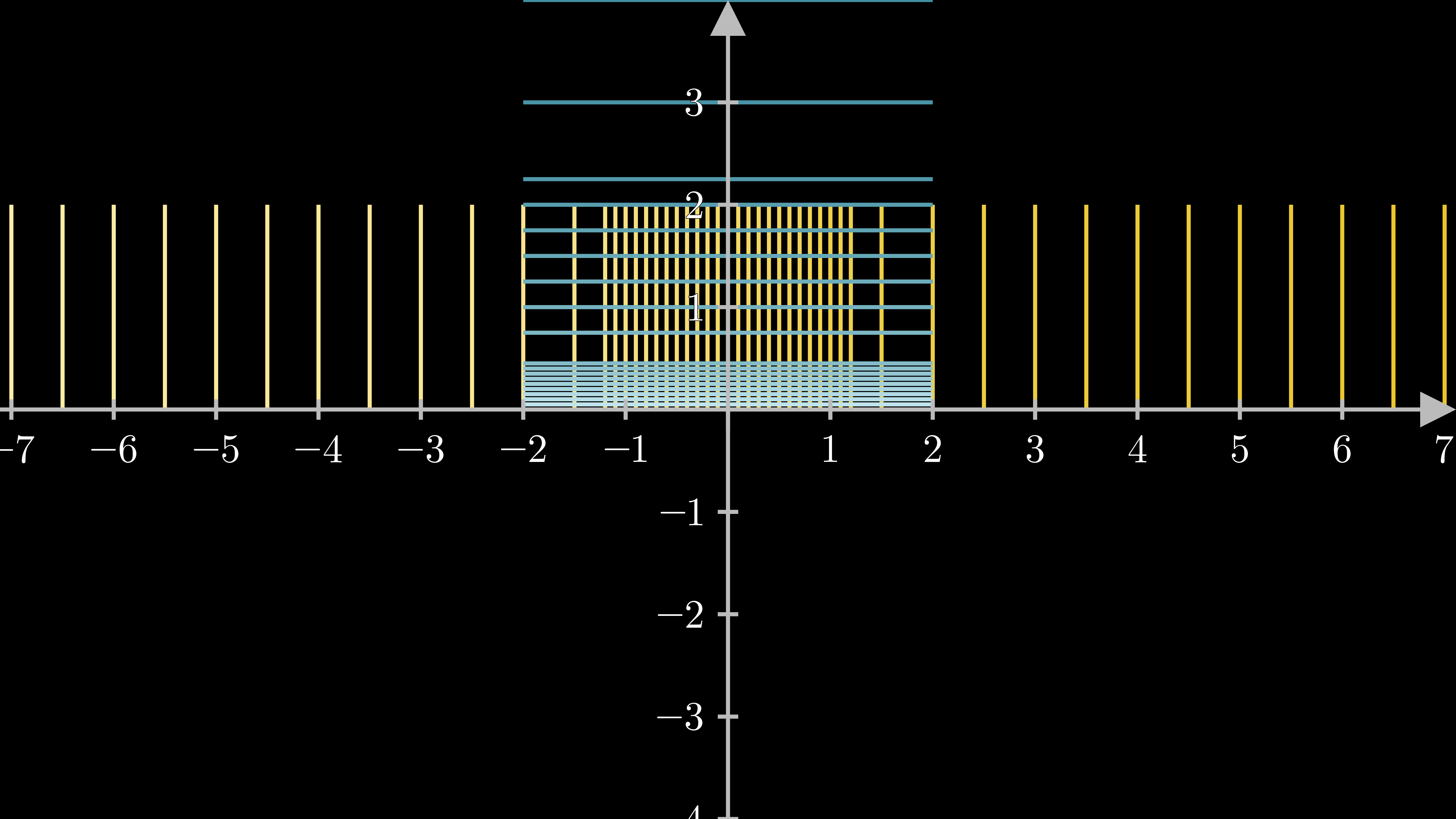
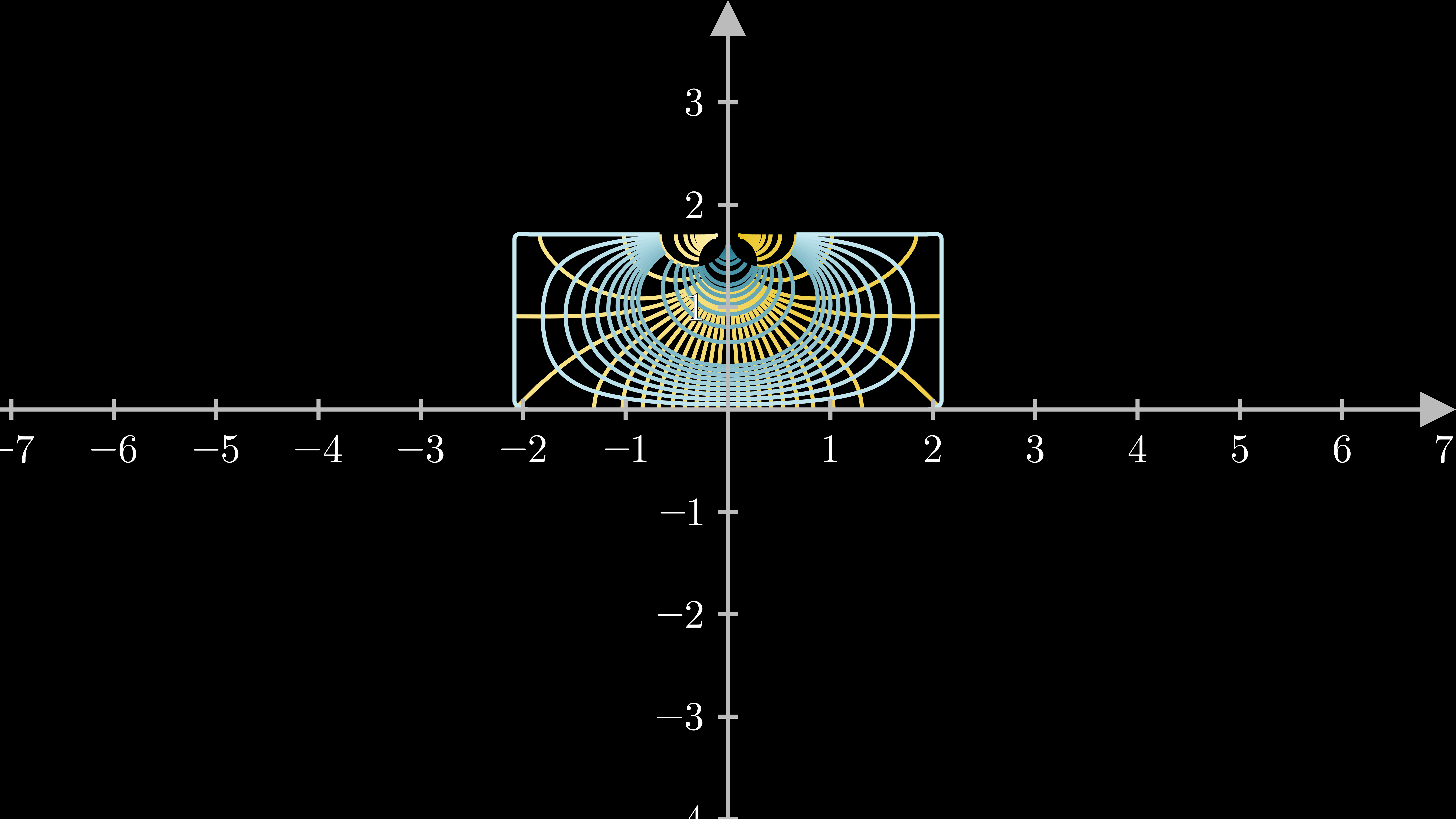
$\quad\\$
椭圆模函数
$\quad\\$
幺模变换$\quad$设椭圆函数$f(z)$的周期模为$M$,若$\forall \omega\in M$可以表示为
$\omega=n_1\omega_1+n_2\omega_2$的形式,则称$(\omega_1,\omega_2)$为$M$的一组基,对$M$的任意两组基
$(\omega_1,\omega_2)$和$(\omega_1’,\omega_2’)$,易知存在整数$a,b,c,d$使得$\displaystyle\begin{pmatrix}\omega_2’\\\omega_1’\end{pmatrix}=\begin{pmatrix}a&b\\c&d\end{pmatrix}\begin{pmatrix}\omega_2\\\omega_1\end{pmatrix}$,
取共轭后等式仍然成立,故有$\displaystyle\begin{pmatrix}\omega_2’&\overline{\omega_2’}\\\omega_1’&\overline{\omega_1’}\end{pmatrix}=\begin{pmatrix}a&b\\c&d\end{pmatrix}\begin{pmatrix}\omega_2&\overline{\omega_2}\\\omega_1&\overline{\omega_1}\end{pmatrix}$,
同理,存在整数$a’,b’,c’,d’$使得
$\displaystyle\begin{pmatrix}\omega_2&\overline{\omega_2}\\\omega_1&\overline{\omega_1}\end{pmatrix}=\begin{pmatrix}a’&b’\\c’&d’\end{pmatrix}\begin{pmatrix}\omega_2’&\overline{\omega_2’}\\\omega_1’&\overline{\omega_1’}\end{pmatrix}$,
因为对任意一组基$(\omega_1,\omega_2)$有$\omega_1\overline{\omega_2}-\omega_2\overline{\omega_1}=\displaystyle 2\text{Im}\frac{\omega_1}{\omega_2}\neq 0$,
故有$\begin{pmatrix}a&b\\c&d\end{pmatrix}\begin{pmatrix}a’&b’\\c’&d’\end{pmatrix}=I_2$,
基变换矩阵互逆,行列式互为倒数,又矩阵元素为整数,易知其行列式为$\pm 1$,称这样的线性变换(系数为整数且行列式为$\pm 1$)为幺模变换,则有
定理8$\quad$同一模的任意两组基由一幺模变换相联系
所有幺模变换构成群$SL_2(\mathbb{Z})$,称为模群
$$\quad\\$$
定义5$\quad$令$\displaystyle\tau=\frac{\omega_2}{\omega_1}$,称满足如下四个条件的$\tau$对应的基$(\omega_1,\omega_2)$为典范基
$(\text{i})\text{Im}\,\tau>0$
$(\text{ii})\displaystyle\frac{1}{2}<\text{Re}\,\tau\le\frac{1}{2}$
$(\text{iii})|\tau|\ge 1$
$(\text{iv})$若$|\tau|=1$,则$\text{Re}\,\tau\ge 0$
$$\quad\\$$
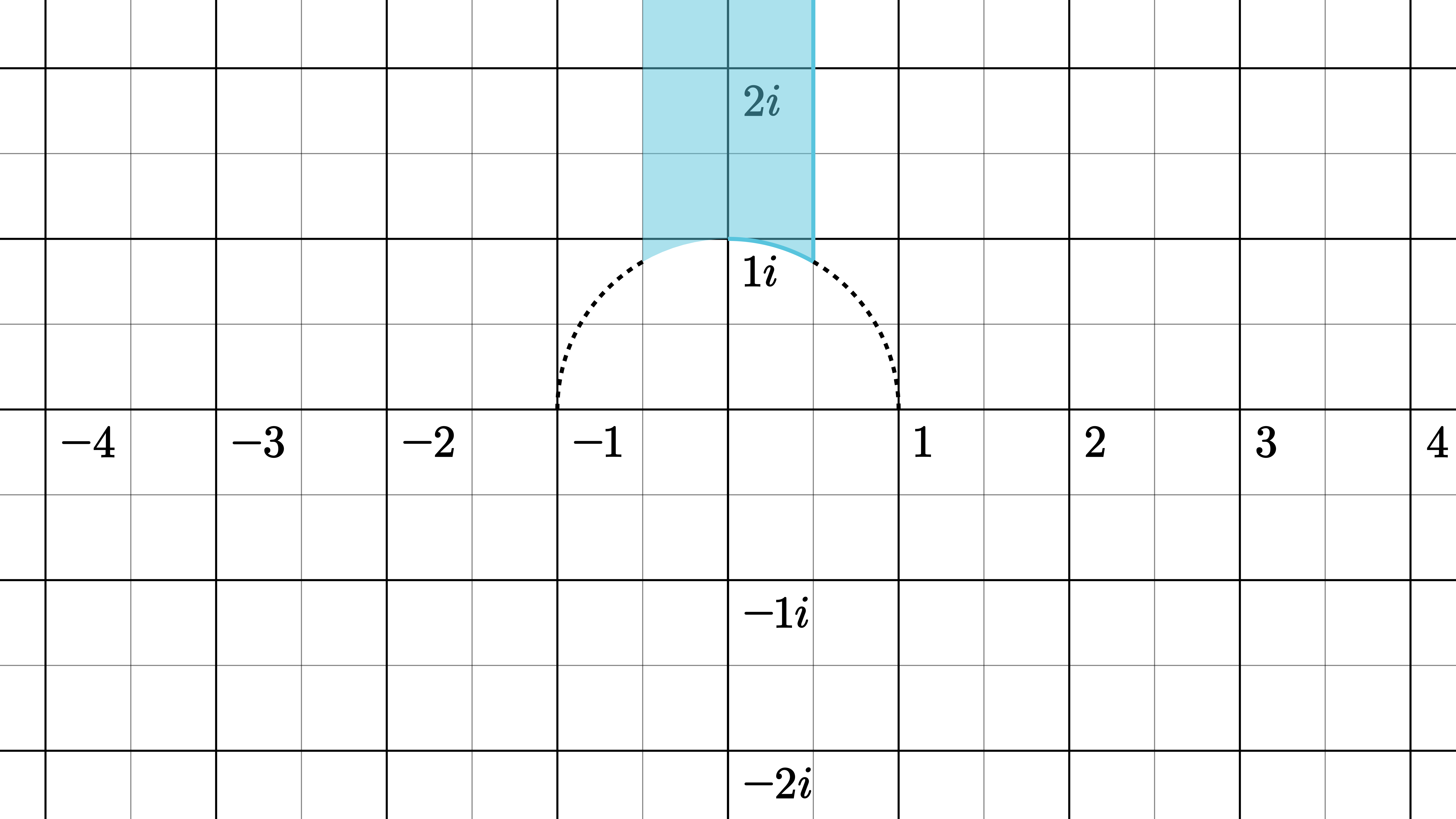
选取$\omega$中模最小且不为零的一个作为$\omega_1$(易知这样的$\omega_1$有两个、四个或六个),不为$\omega_1$整数倍且模最小的为$\omega_2$,可以断言$\displaystyle\tau=\frac{\omega_2}{\omega_1}$不是实数,若其为实数,则有整数$n$使得$n<\tau<n+1$,进而$|n\omega_1-\omega_2|<|\omega_1|$,与$|\omega_1|$最小矛盾,故$\text{Im}\,\tau>0$(否则取$\omega_2$为$-\omega_2$),又$|\omega_2|\le|\omega_1+\omega_2|$,$|\omega_2|\le|\omega_1-\omega_2|$,即$\displaystyle|\text{Re}\,\tau|\le \frac{1}{2}$,若$\displaystyle\text{Re}\,\tau=-\frac{1}{2}$,则令$\omega_2$为$\omega_1+\omega_2$,如此则有$\displaystyle\frac{1}{2}<\text{Re}\,\tau\le\frac{1}{2}$,若$|\tau|=1$且$\text{Re}\,\tau<0$,则将$(\omega_1,\omega_2)$换为$(-\omega_2,\omega_1)$,即满足$\text{Re}\,\tau\ge 0$
由此可知典范基必然存在,且有二、四或者六组,而$\tau$由如上条件唯一确定,几何上,$\tau$属于复平面上如下蓝色区域,称为幺模群的基本域
由上文知基本域中存在一个$\tau$,对其基$(\omega_1,\omega_2)$进行系数为$a,b,c,d$的幺模变换,
易知$\displaystyle\tau’=\frac{a\omega_2+b\omega_1}{c\omega_2+d\omega_1}=\frac{a\tau+b}{c\tau+d}$,
$\displaystyle\text{Im}\,\tau’=\frac{1}{2}\left(\frac{a\tau+b}{c\tau+d}-\frac{a\overline{\tau}+b}{c\overline{\tau}+d}\right)=
(ad-bc)\frac{\text{Im}\,\tau}{|c\tau+d|^2}$,
若$\tau’$位于基本域中,则$ad-bc=1$,由于幺模变换可逆,不妨设$\text{Im}\,\tau’\ge\text{Im}\,\tau$,即$|c\tau+d|\le 1$,由于$c,d$为整数,只有少数几种情况能满足此条件
$(1)d=0,c=\pm 1$,这时$b=\mp 1$,$\tau’=-\displaystyle\frac{1}{\tau}\pm a$,$\displaystyle 1\ge\left|\frac{1}{\tau}\right|=|\tau’\mp a|\ge 1$,即$\displaystyle\left|\frac{1}{\tau}\right|=|\tau’\mp a|=1$,由基本域的形状,$\tau’=\tau=i,a=0$
或$\displaystyle\tau’=\tau=e^{\frac{i\pi }{3}},a=\pm 1$
$(2)d\neq 0$,此时$|c\tau+d|= \sqrt{|c\text{Re}\,\tau+d|^2+\displaystyle\frac{3}{4}c^2}\le 1$,$c=0$或$\pm 1$,
若$c=0$,则$ad=1$,$\tau’=\tau\pm b$,由基本域形状知$\tau’=\tau=i,b=0$
若$c=\pm 1$,则$\displaystyle\text{Re}\, \tau=\frac{1}{2},d=\mp 1,a+b=\mp 1,\tau’=-\frac{1}{\tau-1}\pm a$,
$\displaystyle1\ge\left|\frac{1}{1-\tau}\right|=|\tau’\mp a|\ge 1$,即$\displaystyle\left|\tau-1\right|=|\tau’\mp a|= 1$,
由基本域形状知$\tau’=\tau=e^{\frac{i\pi}{3}},a=0$
综上有
定理9$\quad$基本域中有唯一的$\tau$
$$\quad\\$$
从上文知三个雅可比椭圆函数和$k^2$仅由$\tau$决定,令$\displaystyle\lambda(\tau)=k^2=\frac{e_3-e_2}{e_1-e_2}$,由于$e_1\neq e_2\neq e_3$,易知$\lambda(\tau)$是上半平面$\text{Im}\,\tau>0$上的解析函数,且不取值$0,1$
给定周期模的一组基$(\omega_1,\omega_2)$,则其任何基$(\omega_1’,\omega_2’)$都能通过幺模变换$\begin{pmatrix}a&b\\c&d\end{pmatrix}$
得到,当$a\equiv d\equiv1(\text{mod} \;2),b\equiv c\equiv1(\text{mod} \;2)$时,易知$e_1’,e_2’,e_3’$
分别与$e_1,e_2,e_3$相等,即$\displaystyle\lambda(\tau’)=\lambda(\frac{a\tau+b}{c\tau+d})=\lambda(\tau)$,
满足$\begin{pmatrix}a&b\\c&d\end{pmatrix}(\text{mod} \;2)=\begin{pmatrix}1&0\\0&1\end{pmatrix}$的线性变换构成模群的一个子群,称为同余子群 mod 2,$\lambda(\tau)$在此子群下保持不变,一般地,若一个亚纯函数在线性变换的组成的群下保持不变,则称其为自守函数,若其在模群的子群下保持不变,则称其为模函数,显然,$\lambda(\tau)$是一个椭圆模函数
易知模群$SL_2(\mathbb{Z})$中任何线性变换对应的矩阵模2后都等价于下列六个矩阵之一,且其对$\lambda$的变换如下
| 矩阵 | $\lambda(\tau’)$ | 矩阵 | $\lambda(\tau’)$ |
|---|---|---|---|
| $\begin{pmatrix}1&0\\0&1\end{pmatrix}$ | $\lambda(\tau)$ | $\begin{pmatrix}1&1\\1&0\end{pmatrix}$ | $\displaystyle\frac{\lambda(\tau)-1}{\lambda(\tau)}$ |
| $\begin{pmatrix}0&1\\1&0\end{pmatrix}$ | $1-\lambda(\tau)$ | $\begin{pmatrix}1&0\\1&1\end{pmatrix}$ | $\displaystyle\frac{1}{\lambda(\tau)}$ |
| $\begin{pmatrix}1&1\\0&1\end{pmatrix}$ | $\displaystyle\frac{\lambda(\tau)}{\lambda(\tau)-1}$ | $\begin{pmatrix}0&1\\1&1\end{pmatrix}$ | $\displaystyle\frac{1}{1-\lambda(\tau)}$ |
$$\quad\\$$
$\lambda(\tau)$所作的共形映射$\quad$为方便起见,使用规格化$\omega_1=1,\omega_2=\tau$,此时
$\displaystyle e_3-e_2=\sum_{m,n=-\infty}^{\infty}\left[\frac{1}{\left(m-\displaystyle\frac{1}{2}+\left(n-\displaystyle\frac{1}{2}\right)\tau\right)^2}-\frac{1}{\left(m+\left(n-\displaystyle\frac{1}{2}\right)\tau\right)^2}\right]$
$\displaystyle e_1-e_2=\sum_{m,n=-\infty}^{\infty}\left[\frac{1}{\left(m-\displaystyle\frac{1}{2}+n\tau\right)^2}-\frac{1}{\left(m+\left(n-\displaystyle\frac{1}{2}\right)\tau\right)^2}\right]$
这两个级数均绝对收敛,首先由$n$的对称性知当$\tau$为纯虚数时,$e_1-e_2$与$e_3-e_2$均为实数(对单独的$e_k$亦如此),故$\lambda(\tau)$在虚轴上取实值,其次
$\begin{pmatrix}1&2\\0&1\end{pmatrix}(\text{mod}\; 2)=\begin{pmatrix}1&0\\0&1\end{pmatrix}$,因此$\lambda(\tau+2)=\lambda(\tau)$,即$\lambda(\tau)$有周期$2$,这意味着$\lambda(\tau)$可以表示为$e^{i\pi\tau}$的函数,只需证明当$\text{Im}\,\tau\to\infty$时,$\lambda(\tau)\to 0$,即可确定其傅里叶展开
由公式$\displaystyle\frac{\pi^2}{\sin^2{\pi z}}=\sum_{m=-\infty}^{\infty}\frac{1}{(z-m)^2}$,可以将上两式化为
$\displaystyle e_3-e_2=\pi^2\sum_{n=-\infty}^{\infty}\left[\frac{1}{\cos^2\pi\left(n-\displaystyle\frac{1}{2}\right)\tau}-\frac{1}{\sin^2\pi\left(n-\displaystyle\frac{1}{2}\right)\tau}\right]$
$\displaystyle e_1-e_2=\pi^2\sum_{n=-\infty}^{\infty}\left[\frac{1}{\cos^2\pi n\tau}-\frac{1}{\sin^2\pi\left(n-\displaystyle\frac{1}{2}\right)\tau}\right]$